Master/Project thesis: Improving the CFL limitations of high-fidelity turbulence simulations
Background: High fidelity simulations of turbulence often involve long integration times and lengthy simulations. Given the (inverse) proportionality of the computational cost with time step size, one method to reduce the overall cost is through increasing the time step size, thus requiring fewer time steps for the same overall integration time. In an incompressible solver, the diffusive terms in the equation are often treated implicitly, meaning that the time step size is limited by the CFL condition on the explicit terms, most importantly the convective term.
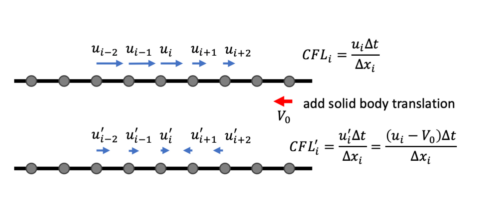
The goal of the proposed project is to get inspiration from the Galilean invariance property of the Navier–Stokes equations and the resulting trick used for canonical flows (such as the channel or pipe flow) and explore whether it is possible to formulate a similar trick to increase the time step size in more generic flow fields. We will start our tests by a simple solver written for the lid-driven cavity flow and expand to more generic Navier–Stokes solvers such as Nek5000/Neko.
Specific tasks:
- Literature review on methods of time integration, different treatments of the convective term, and different tricks used to accelerate time integration.
- Installing and running initial cases with the lid-driven cavity code and Nek5000/Neko.
- Testing the Galilean invariance trick for a few of the more complex flows.
- Coming up with a couple of different tricks to increase time step size.
- Implementation of the methods in lid-driven cavity flow and Nek5000/Neko.
- Simulations using high-performance computing resources.
- Data analysis and reporting of the results.
Requirements:
- Experience and interest in numerical methods
- Strong background in math
- Programming experience in Python/MATLAB and Fortran 77
- Independent working style
Starting date: Immediately, flexible
Advisors: